1.分类

根据已知样本的某些特征，判断一个新的样本属于哪种已知的样本类。

2.分类方法

2.1 逻辑回归

用于解决分类问题的一种模型，根据数据特征或属性，计算其归属于某一类别的概率\(P(x)\)，根据概率数值判断其所属类别。主要应用场景：二分类问题

2.1.1 模型（数学表达式）

\[Y = {1\over 1+e^{-x}} \] \[y = f(x) = \begin{cases} 1, &Y \ge0.5\\ 0, &Y \lt0.5 \end{cases} \]

y为分类结果，P为概率分布函数，x为特征值。

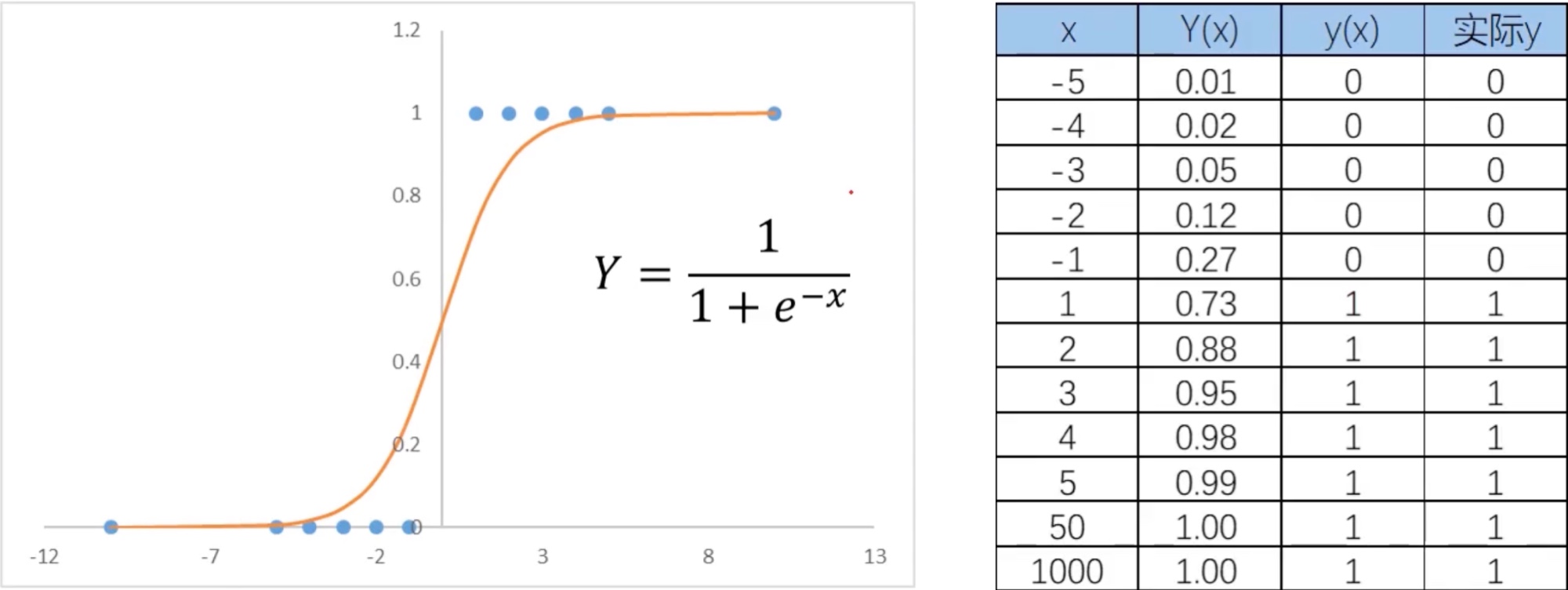
当分类任务变得复杂，例如参数是特征值是2维，3维，则模型将变为如下：

\[Y = {1\over 1+e^{-g(x)}} \] \[g(x) = \theta_0+\theta_1x_1+\theta_2x_2 \]

二阶边界函数

\[g(x) = \theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2+\theta_5x_1x_2 \]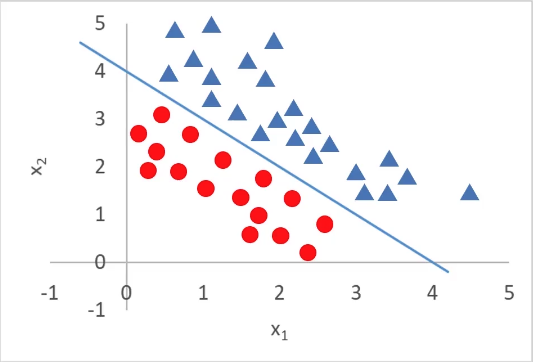

也就是说，需要寻找\(g(x)\)这个边界函数（决策边界）。

2.1.2 最小化损失函数

逻辑回归求解，最小化损失函数（J）:

\[J_i = \begin{cases} -log(P(x_i)), &if\ y_i = 1\\ -log(1-P(x_i)), &if\ y_i = 0 \end{cases} \]

将上面的关系公式转换成下面的关系式，方便在计算机内执行：

\[J = {1\over m}\sum_{i=1}^mJ_i = -{1\over m} \begin{bmatrix} \sum_{i=1}^m(y_ilog(P(x_i))+(1-y_i)log(1-P(x_i))) \end{bmatrix} \]

\(P(x)\)为上面的函数\(Y\)，\(J\)的数值越小，即模型效果越好

2.1.3 逻辑回归实战

模型训练

from sklearn.linear_model import LogisticRegression
lr_model = LogisticRegression()
lr_model.fit(x,y)

边界函数系数

theta1,theta2 = lr_model.coef_[0][0],lr_model.coef[0][1]
theta0 = lr_model.intercept_[0]

对新数据做预测

predictions = lr_model.predict(x_new)

模型评估表现
准确率（类别正确预测的比例）

准确率越接近1越好

\[Accuracy = {正确预测样本数量 \over 总样本数量} \]

第一种：计算准确率

from sklearn.metrics import accuracy_score
y_predict = lr_model.predict(X)
# y是真实的值，y_predict是预测的值
accuracy = accuracy_score(y, y_predict)

第二种：画图看决策边界效果，可视化模型表现

plt.plot(X1, X2_boundary)
passed = plt.scatter(X1[mask], X2[mask])
faild = plt.scatter(X1[~mask], X2[~mask], marker='^')

2.2 KNN近邻模型

选择一个点，然后寻找一定范围内距离其他点的距离，来判断属于那个类别。

2.3 决策树

通过询问一些问题，来最终判定属于那个类别。

2.4 神经网络

3.附录

3.1 图形展示

3.1.1 区分类别的散点图

mask = y == 1
passed = plt.scatter(X1[mask], X2[mask])
failed = plt.scatter(X1[~mask], X2[~mask], marker='^')

3.2 逻辑回归实战（检测芯片质量）

import pandas as pd
import numpy as np
data = pd.read_csv('chip_test.csv')
mask=data.loc[:,'pass']==1

%matplotlib inline 
from matplotlib import pyplot as plt
fig1 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show()

X = data.drop(['pass'],axis=1)
y = data.loc[:,'pass']
X1 = data.loc[:,'test1']
X2 = data.loc[:,'test2']
X1.head()
#create new data
X1_2 = X1*X1
X2_2 = X2*X2
X1_X2 = X1*X2
X_new = {'X1':X1,'X2':X2,'X1_2':X1_2,'X2_2':X2_2,'X1_X2':X1_X2}
X_new = pd.DataFrame(X_new)

from sklearn.linear_model import LogisticRegression
LR2 = LogisticRegression()
LR2.fit(X_new,y)

from sklearn.metrics import accuracy_score
y2_predict = LR2.predict(X_new)
accuracy2 = accuracy_score(y,y2_predict)
print(accuracy2)

X1_new = X1.sort_values()
theta0 = LR2.intercept_
theta1,theta2,theta3,theta4,theta5 = LR2.coef_[0][0],LR2.coef_[0][1],LR2.coef_[0][2],LR2.coef_[0][3],LR2.coef_[0][4]
a = theta4
b = theta5*X1_new+theta2
c = theta0+theta1*X1_new+theta3*X1_new*X1_new
X2_new_boundary = (-b+np.sqrt(b*b-4*a*c))/(2*a)

fig2 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.plot(X1_new,X2_new_boundary)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show()

def f(x):
    a = theta4
    b = theta5*x+theta2
    c = theta0+theta1*x+theta3*x*x
    X2_new_boundary1 = (-b+np.sqrt(b*b-4*a*c))/(2*a)
    X2_new_boundary2 = (-b-np.sqrt(b*b-4*a*c))/(2*a)
    return X2_new_boundary1,X2_new_boundary2
    
X2_new_boundary1 = []
X2_new_boundary2 = []
for x in X1_new:
    X2_new_boundary1.append(f(x)[0])
    X2_new_boundary2.append(f(x)[1])
print(X2_new_boundary1,X2_new_boundary2)

fig3 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.plot(X1_new,X2_new_boundary1)
plt.plot(X1_new,X2_new_boundary2)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show()

X1_range = [-0.9 + x/10000 for x in range(0,19000)]
X1_range = np.array(X1_range)
X2_new_boundary1 = []
X2_new_boundary2 = []
for x in X1_range:
    X2_new_boundary1.append(f(x)[0])
    X2_new_boundary2.append(f(x)[1])

import matplotlib as mlp
mlp.rcParams['font.family'] = 'SimHei'
mlp.rcParams['axes.unicode_minus'] = False
fig4 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.plot(X1_range,X2_new_boundary1,'r')
plt.plot(X1_range,X2_new_boundary2,'r')
plt.title('test1-test2')
plt.xlabel('测试1')
plt.ylabel('测试2')
plt.title('芯片质量预测')
plt.legend((passed,failed),('passed','failed'))
plt.show()